The standard Gaussian kernel. More...

Public Member Functions
	GaussianKernel ()
	Default constructor; sets bandwidth to 1.0. More...

	GaussianKernel (const double bandwidth)
	Construct the Gaussian kernel with a custom bandwidth. More...

double	Bandwidth () const
	Get the bandwidth. More...

void	Bandwidth (const double bandwidth)
	Modify the bandwidth. More...

template<typename VecTypeA , typename VecTypeB >
double	ConvolutionIntegral (const VecTypeA &a, const VecTypeB &b)
	Obtain a convolution integral of the Gaussian kernel. More...

template<typename VecTypeA , typename VecTypeB >
double	Evaluate (const VecTypeA &a, const VecTypeB &b) const
	Evaluation of the Gaussian kernel. More...

double	Evaluate (const double t) const
	Evaluation of the Gaussian kernel given the distance between two points. More...

double	Gamma () const
	Get the precalculated constant. More...

double	Gradient (const double t) const
	Evaluation of the gradient of Gaussian kernel given the distance between two points. More...

double	GradientForSquaredDistance (const double t) const
	Evaluation of the gradient of Gaussian kernel given the squared distance between two points. More...

double	Normalizer (const size_t dimension)
	Obtain the normalization constant of the Gaussian kernel. More...

template<typename Archive >
void	Serialize (Archive &ar, const unsigned int)
	Serialize the kernel. More...

Private Attributes
double	bandwidth
	Kernel bandwidth. More...

double	gamma
	Precalculated constant depending on the bandwidth; 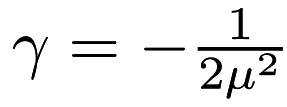$\gamma = -\frac{1}{2 \mu^2}$ . More...

Detailed Description

The standard Gaussian kernel.

Given two vectors 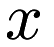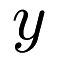$ x $ , $ y $ , and a bandwidth 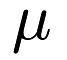$\mu$ (set in the constructor),

$K(x, y) = \exp(-\frac{|| x - y ||^2}{2 \mu^2}).$

The implementation is all in the header file because it is so simple.

Definition at line 34 of file gaussian_kernel.hpp.

Constructor & Destructor Documentation

mlpack::kernel::GaussianKernel::GaussianKernel ( )

inline

Default constructor; sets bandwidth to 1.0.

Definition at line 40 of file gaussian_kernel.hpp.

mlpack::kernel::GaussianKernel::GaussianKernel ( const double bandwidth )

inline

Construct the Gaussian kernel with a custom bandwidth.

Parameters

bandwidth The bandwidth of the kernel ( 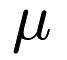$\mu$ ).

Definition at line 48 of file gaussian_kernel.hpp.

Member Function Documentation

double mlpack::kernel::GaussianKernel::Bandwidth ( ) const

inline

Get the bandwidth.

Definition at line 135 of file gaussian_kernel.hpp.

References bandwidth.

void mlpack::kernel::GaussianKernel::Bandwidth ( const double bandwidth )

inline

Modify the bandwidth.

This takes an argument because we must update the precalculated constant (gamma).

Definition at line 139 of file gaussian_kernel.hpp.

References bandwidth, and gamma.

template<typename VecTypeA , typename VecTypeB >

double mlpack::kernel::GaussianKernel::ConvolutionIntegral	(	const VecTypeA &	a,
		const VecTypeB &	b
	)

inline

Obtain a convolution integral of the Gaussian kernel.

Parameters

a	First vector.
b	Second vector.

Returns: The convolution integral.

Definition at line 127 of file gaussian_kernel.hpp.

References Evaluate(), mlpack::metric::LMetric< TPower, TTakeRoot >::Evaluate(), and Normalizer().

template<typename VecTypeA , typename VecTypeB >

double mlpack::kernel::GaussianKernel::Evaluate	(	const VecTypeA &	a,
		const VecTypeB &	b
	)		const

inline

Evaluation of the Gaussian kernel.

This could be generalized to use any distance metric, not the Euclidean distance, but for now, the Euclidean distance is used.

Template Parameters

VecType Type of vector (likely arma::vec or arma::spvec).

Parameters

a	First vector.
b	Second vector.

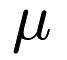Returns: K(a, b) using the bandwidth ( $\mu$ ) specified in the constructor.

Definition at line 65 of file gaussian_kernel.hpp.

References mlpack::metric::LMetric< TPower, TTakeRoot >::Evaluate(), and gamma.

Referenced by ConvolutionIntegral().

double mlpack::kernel::GaussianKernel::Evaluate ( const double t ) const

inline

Evaluation of the Gaussian kernel given the distance between two points.

Parameters

t	The distance between the two points the kernel is evaluated on.

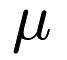Returns: K(t) using the bandwidth ( $\mu$ ) specified in the constructor.

Definition at line 78 of file gaussian_kernel.hpp.

References gamma.

double mlpack::kernel::GaussianKernel::Gamma ( ) const

inline

Get the precalculated constant.

Definition at line 146 of file gaussian_kernel.hpp.

References gamma.

double mlpack::kernel::GaussianKernel::Gradient ( const double t ) const

inline

Evaluation of the gradient of Gaussian kernel given the distance between two points.

Parameters

t	The distance between the two points the kernel is evaluated on.

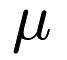Returns: K(t) using the bandwidth ( $\mu$ ) specified in the constructor.

Definition at line 92 of file gaussian_kernel.hpp.

References gamma.

double mlpack::kernel::GaussianKernel::GradientForSquaredDistance ( const double t ) const

inline

Evaluation of the gradient of Gaussian kernel given the squared distance between two points.

Parameters

t	The squared distance between the two points

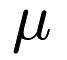Returns: K(t) using the bandwidth ( $\mu$ ) specified in the constructor.

Definition at line 104 of file gaussian_kernel.hpp.

References gamma.

double mlpack::kernel::GaussianKernel::Normalizer ( const size_t dimension )

inline

Obtain the normalization constant of the Gaussian kernel.

Parameters

dimension

Returns: the normalization constant

Definition at line 114 of file gaussian_kernel.hpp.

References bandwidth, and M_PI.

Referenced by ConvolutionIntegral().

template<typename Archive >

void mlpack::kernel::GaussianKernel::Serialize	(	Archive &	ar,
		const unsigned	int
	)

inline

Serialize the kernel.

Definition at line 150 of file gaussian_kernel.hpp.

References bandwidth, mlpack::data::CreateNVP(), and gamma.

Member Data Documentation

double mlpack::kernel::GaussianKernel::bandwidth

private

Kernel bandwidth.

Definition at line 158 of file gaussian_kernel.hpp.

Referenced by Bandwidth(), Normalizer(), and Serialize().

double mlpack::kernel::GaussianKernel::gamma

private

Precalculated constant depending on the bandwidth; 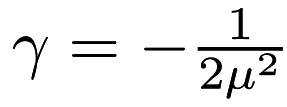$\gamma = -\frac{1}{2 \mu^2}$ .

Definition at line 162 of file gaussian_kernel.hpp.

Referenced by Bandwidth(), Evaluate(), Gamma(), Gradient(), GradientForSquaredDistance(), and Serialize().

The documentation for this class was generated from the following file:

src/mlpack/core/kernels/gaussian_kernel.hpp

Public Member Functions

Private Attributes

Detailed Description

Constructor & Destructor Documentation

Member Function Documentation

Member Data Documentation