An implementation of LARS, a stage-wise homotopy-based algorithm for l1-regularized linear regression (LASSO) and l1+l2 regularized linear regression (Elastic Net). More...

Public Member Functions
	LARS (const bool useCholesky=false, const double lambda1=0.0, const double lambda2=0.0, const double tolerance=1e-16)
	Set the parameters to LARS. More...

	LARS (const bool useCholesky, const arma::mat &gramMatrix, const double lambda1=0.0, const double lambda2=0.0, const double tolerance=1e-16)
	Set the parameters to LARS, and pass in a precalculated Gram matrix. More...

const std::vector< size_t > &	ActiveSet () const
	Access the set of active dimensions. More...

const std::vector< arma::vec > &	BetaPath () const
	Access the set of coefficients after each iteration; the solution is the last element. More...

const std::vector< double > &	LambdaPath () const
	Access the set of values for lambda1 after each iteration; the solution is the last element. More...

const arma::mat &	MatUtriCholFactor () const
	Access the upper triangular cholesky factor. More...

void	Predict (const arma::mat &points, arma::vec &predictions, const bool rowMajor=false) const
	Predict y_i for each data point in the given data matrix, using the currently-trained LARS model (so make sure you run Regress() first). More...

template<typename Archive >
void	Serialize (Archive &ar, const unsigned int)
	Serialize the LARS model. More...

void	Train (const arma::mat &data, const arma::vec &responses, arma::vec &beta, const bool transposeData=true)
	Run LARS. More...

Private Member Functions
void	Activate (const size_t varInd)
	Add dimension varInd to active set. More...

void	CholeskyDelete (const size_t colToKill)

void	CholeskyInsert (const arma::vec &newX, const arma::mat &X)

void	CholeskyInsert (double sqNormNewX, const arma::vec &newGramCol)

void	ComputeYHatDirection (const arma::mat &matX, const arma::vec &betaDirection, arma::vec &yHatDirection)

void	Deactivate (const size_t activeVarInd)
	Remove activeVarInd'th element from active set. More...

void	GivensRotate (const arma::vec::fixed< 2 > &x, arma::vec::fixed< 2 > &rotatedX, arma::mat &G)

void	Ignore (const size_t varInd)
	Add dimension varInd to ignores set (never removed). More...

void	InterpolateBeta ()

Private Attributes
std::vector< size_t >	activeSet
	Active set of dimensions. More...

std::vector< arma::vec >	betaPath
	Solution path. More...

bool	elasticNet
	True if this is the elastic net problem. More...

std::vector< size_t >	ignoreSet
	Set of ignored variables (for dimensions in span{active set dimensions}). More...

std::vector< bool >	isActive
	Active set membership indicator (for each dimension). More...

std::vector< bool >	isIgnored
	Membership indicator for set of ignored variables. More...

double	lambda1
	Regularization parameter for l1 penalty. More...

double	lambda2
	Regularization parameter for l2 penalty. More...

std::vector< double >	lambdaPath
	Value of lambda_1 for each solution in solution path. More...

bool	lasso
	True if this is the LASSO problem. More...

const arma::mat *	matGram
	Pointer to the Gram matrix we will use. More...

arma::mat	matGramInternal
	Gram matrix. More...

arma::mat	matUtriCholFactor
	Upper triangular cholesky factor; initially 0x0 matrix. More...

double	tolerance
	Tolerance for main loop. More...

bool	useCholesky
	Whether or not to use Cholesky decomposition when solving linear system. More...

Detailed Description

An implementation of LARS, a stage-wise homotopy-based algorithm for l1-regularized linear regression (LASSO) and l1+l2 regularized linear regression (Elastic Net).

Let 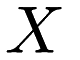$ X $ be a matrix where each row is a point and each column is a dimension and let 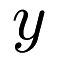$ y $ be a vector of responses.

The Elastic Net problem is to solve

$\min_{\beta} 0.5 || X \beta - y ||_2^2 + \lambda_1 || \beta ||_1 + 0.5 \lambda_2 || \beta ||_2^2$

where $\beta$ is the vector of regression coefficients.

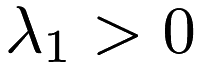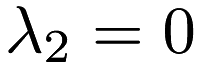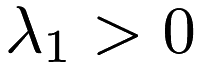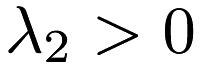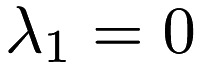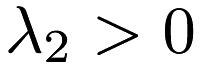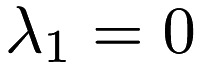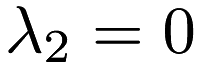If $\lambda_1 > 0$ and $\lambda_2 = 0$ , the problem is the LASSO. If $\lambda_1 > 0$ and $\lambda_2 > 0$ , the problem is the elastic net. If $\lambda_1 = 0$ and $\lambda_2 > 0$ , the problem is ridge regression. If $\lambda_1 = 0$ and $\lambda_2 = 0$ , the problem is unregularized linear regression.

Note: This algorithm is not recommended for use (in terms of efficiency) when 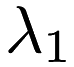$\lambda_1$ = 0.

For more details, see the following papers:

@article{efron2004least,
  title={Least angle regression},
  author={Efron, B. and Hastie, T. and Johnstone, I. and Tibshirani, R.},
  journal={The Annals of statistics},
  volume={32},
  number={2},
  pages={407--499},
  year={2004},
  publisher={Institute of Mathematical Statistics}
}

@article{zou2005regularization,
  title={Regularization and variable selection via the elastic net},
  author={Zou, H. and Hastie, T.},
  journal={Journal of the Royal Statistical Society Series B},
  volume={67},
  number={2},
  pages={301--320},
  year={2005},
  publisher={Royal Statistical Society}
}

Definition at line 89 of file lars.hpp.

Constructor & Destructor Documentation

mlpack::regression::LARS::LARS	(	const bool	useCholesky = `false`,
		const double	lambda1 = `0.0`,
		const double	lambda2 = `0.0`,
		const double	tolerance = `1e-16`
	)

Set the parameters to LARS.

Both lambda1 and lambda2 default to 0.

Parameters

useCholesky	Whether or not to use Cholesky decomposition when solving linear system (as opposed to using the full Gram matrix).
lambda1	Regularization parameter for l1-norm penalty.
lambda2	Regularization parameter for l2-norm penalty.
tolerance	Run until the maximum correlation of elements in (X^T y) is less than this.

mlpack::regression::LARS::LARS	(	const bool	useCholesky,
		const arma::mat &	gramMatrix,
		const double	lambda1 = `0.0`,
		const double	lambda2 = `0.0`,
		const double	tolerance = `1e-16`
	)

Set the parameters to LARS, and pass in a precalculated Gram matrix.

Both lambda1 and lambda2 default to 0.

Parameters

useCholesky	Whether or not to use Cholesky decomposition when solving linear system (as opposed to using the full Gram matrix).
gramMatrix	Gram matrix.
lambda1	Regularization parameter for l1-norm penalty.
lambda2	Regularization parameter for l2-norm penalty.
tolerance	Run until the maximum correlation of elements in (X^T y) is less than this.

Member Function Documentation

void mlpack::regression::LARS::Activate ( const size_t varInd )

private

Add dimension varInd to active set.

Parameters

varInd Dimension to add to active set.

const std::vector<size_t>& mlpack::regression::LARS::ActiveSet ( ) const

inline

Access the set of active dimensions.

Definition at line 158 of file lars.hpp.

References activeSet.

const std::vector<arma::vec>& mlpack::regression::LARS::BetaPath ( ) const

inline

Access the set of coefficients after each iteration; the solution is the last element.

Definition at line 162 of file lars.hpp.

References betaPath.

void mlpack::regression::LARS::CholeskyDelete ( const size_t colToKill )

private

void mlpack::regression::LARS::CholeskyInsert	(	const arma::vec &	newX,
		const arma::mat &	X
	)

private

void mlpack::regression::LARS::CholeskyInsert	(	double	sqNormNewX,
		const arma::vec &	newGramCol
	)

private

void mlpack::regression::LARS::ComputeYHatDirection	(	const arma::mat &	matX,
		const arma::vec &	betaDirection,
		arma::vec &	yHatDirection
	)

private

void mlpack::regression::LARS::Deactivate ( const size_t activeVarInd )

private

Remove activeVarInd'th element from active set.

Parameters

activeVarInd Index of element to remove from active set.

void mlpack::regression::LARS::GivensRotate	(	const arma::vec::fixed< 2 > &	x,
		arma::vec::fixed< 2 > &	rotatedX,
		arma::mat &	G
	)

private

void mlpack::regression::LARS::Ignore ( const size_t varInd )

private

Add dimension varInd to ignores set (never removed).

Parameters

varInd Dimension to add to ignores set.

void mlpack::regression::LARS::InterpolateBeta ( )

private

const std::vector<double>& mlpack::regression::LARS::LambdaPath ( ) const

inline

Access the set of values for lambda1 after each iteration; the solution is the last element.

Definition at line 166 of file lars.hpp.

References lambdaPath.

const arma::mat& mlpack::regression::LARS::MatUtriCholFactor ( ) const

inline

Access the upper triangular cholesky factor.

Definition at line 169 of file lars.hpp.

References matUtriCholFactor, and Serialize().

void mlpack::regression::LARS::Predict	(	const arma::mat &	points,
		arma::vec &	predictions,
		const bool	rowMajor = `false`
	)		const

Predict y_i for each data point in the given data matrix, using the currently-trained LARS model (so make sure you run Regress() first).

If the data matrix is row-major (as opposed to the usual column-major format for mlpack matrices), set rowMajor = true to avoid an extra transpose.

Parameters

points	The data points to regress on.
predictions	y, which will contained calculated values on completion.

template<typename Archive >

void mlpack::regression::LARS::Serialize	(	Archive &	ar,
		const unsigned	int
	)

Serialize the LARS model.

Referenced by MatUtriCholFactor().

void mlpack::regression::LARS::Train	(	const arma::mat &	data,
		const arma::vec &	responses,
		arma::vec &	beta,
		const bool	transposeData = `true`
	)

Run LARS.

The input matrix (like all mlpack matrices) should be column-major – each column is an observation and each row is a dimension. However, because LARS is more efficient on a row-major matrix, this method will (internally) transpose the matrix. If this transposition is not necessary (i.e., you want to pass in a row-major matrix), pass 'false' for the transposeData parameter.

Parameters

data	Column-major input data (or row-major input data if rowMajor = true).
responses	A vector of targets.
beta	Vector to store the solution (the coefficients) in.
transposeData	Set to false if the data is row-major.

Member Data Documentation

std::vector<size_t> mlpack::regression::LARS::activeSet

private

Active set of dimensions.

Definition at line 210 of file lars.hpp.

Referenced by ActiveSet().

std::vector<arma::vec> mlpack::regression::LARS::betaPath

private

Solution path.

Definition at line 204 of file lars.hpp.

Referenced by BetaPath().

bool mlpack::regression::LARS::elasticNet

private

True if this is the elastic net problem.

Definition at line 196 of file lars.hpp.

std::vector<size_t> mlpack::regression::LARS::ignoreSet

private

Set of ignored variables (for dimensions in span{active set dimensions}).

Definition at line 218 of file lars.hpp.

std::vector<bool> mlpack::regression::LARS::isActive

private

Active set membership indicator (for each dimension).

Definition at line 213 of file lars.hpp.

std::vector<bool> mlpack::regression::LARS::isIgnored

private

Membership indicator for set of ignored variables.

Definition at line 221 of file lars.hpp.

double mlpack::regression::LARS::lambda1

private

Regularization parameter for l1 penalty.

Definition at line 193 of file lars.hpp.

double mlpack::regression::LARS::lambda2

private

Regularization parameter for l2 penalty.

Definition at line 198 of file lars.hpp.

std::vector<double> mlpack::regression::LARS::lambdaPath

private

Value of lambda_1 for each solution in solution path.

Definition at line 207 of file lars.hpp.

Referenced by LambdaPath().

bool mlpack::regression::LARS::lasso

private

True if this is the LASSO problem.

Definition at line 191 of file lars.hpp.

const arma::mat* mlpack::regression::LARS::matGram

private

Pointer to the Gram matrix we will use.

Definition at line 182 of file lars.hpp.

arma::mat mlpack::regression::LARS::matGramInternal

private

Gram matrix.

Definition at line 179 of file lars.hpp.

arma::mat mlpack::regression::LARS::matUtriCholFactor

private

Upper triangular cholesky factor; initially 0x0 matrix.

Definition at line 185 of file lars.hpp.

Referenced by MatUtriCholFactor().

double mlpack::regression::LARS::tolerance

private

Tolerance for main loop.

Definition at line 201 of file lars.hpp.

bool mlpack::regression::LARS::useCholesky

private

Whether or not to use Cholesky decomposition when solving linear system.

Definition at line 188 of file lars.hpp.

The documentation for this class was generated from the following file:

src/mlpack/methods/lars/lars.hpp

Public Member Functions

Private Member Functions

Private Attributes

Detailed Description

Constructor & Destructor Documentation

Member Function Documentation

Member Data Documentation