|
mlpack
master
|
The Mahalanobis distance, which is essentially a stretched Euclidean distance. More...
Public Member Functions | |
| MahalanobisDistance () | |
| Initialize the Mahalanobis distance with the empty matrix as covariance. More... | |
| MahalanobisDistance (const size_t dimensionality) | |
| Initialize the Mahalanobis distance with the identity matrix of the given dimensionality. More... | |
| MahalanobisDistance (const arma::mat &covariance) | |
| Initialize the Mahalanobis distance with the given covariance matrix. More... | |
| const arma::mat & | Covariance () const |
| Access the covariance matrix. More... | |
| arma::mat & | Covariance () |
| Modify the covariance matrix. More... | |
| template<typename VecTypeA , typename VecTypeB > | |
| double | Evaluate (const VecTypeA &a, const VecTypeB &b) |
| Evaluate the distance between the two given points using this Mahalanobis distance. More... | |
| template<typename Archive > | |
| void | Serialize (Archive &ar, const unsigned int version) |
| Serialize the Mahalanobis distance. More... | |
Private Attributes | |
| arma::mat | covariance |
| The covariance matrix associated with this distance. More... | |
The Mahalanobis distance, which is essentially a stretched Euclidean distance.
Given a square covariance matrix 
of size 
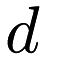x 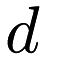, where 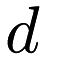is the dimensionality of the points it will be evaluating, and given two vectors 
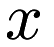and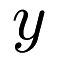 
also of dimensionality ,
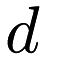![\[ d(x, y) = \sqrt{(x - y)^T Q (x - y)} \]](form_31.png)
where Q is the covariance matrix.
Because each evaluation multiplies (x_1 - x_2) by the covariance matrix, it may be much quicker to use an LMetric and simply stretch the actual dataset itself before performing any evaluations. However, this class is provided for convenience.
Similar to the LMetric class, this offers a template parameter TakeRoot which, when set to false, will instead evaluate the distance
![\[ d(x, y) = (x - y)^T Q (x - y) \]](form_32.png)
which is faster to evaluate.
| TakeRoot | If true, takes the root of the output. It is slightly faster to leave this at the default of false, but this means the metric may not satisfy the triangle inequality and may not be usable for methods that expect a true metric. |
Definition at line 53 of file mahalanobis_distance.hpp.
|
inline |
Initialize the Mahalanobis distance with the empty matrix as covariance.
Don't call Evaluate() until you set the covariance with Covariance()!
Definition at line 60 of file mahalanobis_distance.hpp.
|
inline |
Initialize the Mahalanobis distance with the identity matrix of the given dimensionality.
| dimensionality | Dimesnsionality of the covariance matrix. |
Definition at line 68 of file mahalanobis_distance.hpp.
|
inline |
Initialize the Mahalanobis distance with the given covariance matrix.
The given covariance matrix will be copied (this is not optimal).
| covariance | The covariance matrix to use for this distance. |
Definition at line 77 of file mahalanobis_distance.hpp.
References mlpack::metric::MahalanobisDistance< TakeRoot >::Evaluate().
|
inline |
Access the covariance matrix.
Definition at line 96 of file mahalanobis_distance.hpp.
References mlpack::metric::MahalanobisDistance< TakeRoot >::covariance.
|
inline |
Modify the covariance matrix.
Definition at line 103 of file mahalanobis_distance.hpp.
References mlpack::metric::MahalanobisDistance< TakeRoot >::covariance, and mlpack::metric::MahalanobisDistance< TakeRoot >::Serialize().
| double mlpack::metric::MahalanobisDistance< TakeRoot >::Evaluate | ( | const VecTypeA & | a, |
| const VecTypeB & | b | ||
| ) |
Evaluate the distance between the two given points using this Mahalanobis distance.
If the covariance matrix has not been set (i.e. if you used the empty constructor and did not later modify the covariance matrix), calling this method will probably result in a crash.
| a | First vector. |
| b | Second vector. |
Referenced by mlpack::metric::MahalanobisDistance< TakeRoot >::MahalanobisDistance().
| void mlpack::metric::MahalanobisDistance< TakeRoot >::Serialize | ( | Archive & | ar, |
| const unsigned int | version | ||
| ) |
Serialize the Mahalanobis distance.
Referenced by mlpack::metric::MahalanobisDistance< TakeRoot >::Covariance().
|
private |
The covariance matrix associated with this distance.
Definition at line 111 of file mahalanobis_distance.hpp.
Referenced by mlpack::metric::MahalanobisDistance< TakeRoot >::Covariance().
1.8.11
