mlpack::kernel::EpanechnikovKernel Class Reference

The Epanechnikov kernel, defined as. More...

Public Member Functions
	EpanechnikovKernel (const double bandwidth=1.0)
	Instantiate the Epanechnikov kernel with the given bandwidth (default 1.0). More...
template<typename VecTypeA , typename VecTypeB >
double	ConvolutionIntegral (const VecTypeA &a, const VecTypeB &b)
	Obtains the convolution integral [integral of K(||x-a||) K(||b-x||) dx] for the two vectors. More...
template<typename VecTypeA , typename VecTypeB >
double	Evaluate (const VecTypeA &a, const VecTypeB &b) const
	Evaluate the Epanechnikov kernel on the given two inputs. More...
double	Evaluate (const double distance) const
	Evaluate the Epanechnikov kernel given that the distance between the two input points is known. More...
double	Gradient (const double distance) const
	Evaluate the Gradient of Epanechnikov kernel given that the distance between the two input points is known. More...
double	GradientForSquaredDistance (const double distanceSquared) const
	Evaluate the Gradient of Epanechnikov kernel given that the squared distance between the two input points is known. More...
double	Normalizer (const size_t dimension)
	Compute the normalizer of this Epanechnikov kernel for the given dimension. More...
template<typename Archive >
void	Serialize (Archive &ar, const unsigned int version)
	Serialize the kernel. More...

Private Attributes
double	bandwidth
	Bandwidth of the kernel. More...
double	inverseBandwidthSquared
	Cached value of the inverse bandwidth squared (to speed up computation). More...

Detailed Description

The Epanechnikov kernel, defined as.

where 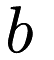is the bandwidth the of the kernel (defaults to 1.0).

Definition at line 30 of file epanechnikov_kernel.hpp.

Constructor & Destructor Documentation

mlpack::kernel::EpanechnikovKernel::EpanechnikovKernel ( const double  bandwidth = 1.0 )

inline

Instantiate the Epanechnikov kernel with the given bandwidth (default 1.0).

Parameters

bandwidth

Bandwidth of the kernel.

Definition at line 38 of file epanechnikov_kernel.hpp.

References ConvolutionIntegral(), Evaluate(), Gradient(), GradientForSquaredDistance(), Normalizer(), and Serialize().

Member Function Documentation

template<typename VecTypeA , typename VecTypeB >

double mlpack::kernel::EpanechnikovKernel::ConvolutionIntegral	(	const VecTypeA &	a,
		const VecTypeB &	b
	)

Obtains the convolution integral [integral of K(||x-a||) K(||b-x||) dx] for the two vectors.

Template Parameters

VecType

Type of vector (arma::vec, arma::spvec should be expected).

Parameters

a	First vector.
b	Second vector.

Returns

the convolution integral value.

Referenced by EpanechnikovKernel().

template<typename VecTypeA , typename VecTypeB >

double mlpack::kernel::EpanechnikovKernel::Evaluate	(	const VecTypeA &	a,
		const VecTypeB &	b
	)		const

Evaluate the Epanechnikov kernel on the given two inputs.

Template Parameters

VecTypeA	Type of first vector.
VecTypeB	Type of second vector.

Parameters

a	One input vector.
b	The other input vector.

Referenced by EpanechnikovKernel().

double mlpack::kernel::EpanechnikovKernel::Evaluate

(

const double

distance

)

const

Evaluate the Epanechnikov kernel given that the distance between the two input points is known.

double mlpack::kernel::EpanechnikovKernel::Gradient

(

const double

distance

)

const

Evaluate the Gradient of Epanechnikov kernel given that the distance between the two input points is known.

Referenced by EpanechnikovKernel().

double mlpack::kernel::EpanechnikovKernel::GradientForSquaredDistance

(

const double

distanceSquared

)

const

Evaluate the Gradient of Epanechnikov kernel given that the squared distance between the two input points is known.

Referenced by EpanechnikovKernel().

double mlpack::kernel::EpanechnikovKernel::Normalizer

(

const size_t

dimension

)

Compute the normalizer of this Epanechnikov kernel for the given dimension.

Parameters

dimension

Dimension to calculate the normalizer for.

Referenced by EpanechnikovKernel().

template<typename Archive >

void mlpack::kernel::EpanechnikovKernel::Serialize	(	Archive &	ar,
		const unsigned int	version
	)

Serialize the kernel.

Referenced by EpanechnikovKernel().

Member Data Documentation

double mlpack::kernel::EpanechnikovKernel::bandwidth

private

Bandwidth of the kernel.

Definition at line 100 of file epanechnikov_kernel.hpp.

double mlpack::kernel::EpanechnikovKernel::inverseBandwidthSquared

private

Cached value of the inverse bandwidth squared (to speed up computation).

Definition at line 102 of file epanechnikov_kernel.hpp.

---

The documentation for this class was generated from the following file:

• src/mlpack/core/kernels/epanechnikov_kernel.hpp